mécanique hydraulique
I. CONTRAINTES EFFECTIVES ET TOTALESI.1. Postulat de Terzaghi
L’idée fondamentale de Terzaghi consiste à postuler
l’existence d’un nouveau tenseur de contraintes (au lieu du tenseur de
contraintes en chaque point du sol calculé de la même façon qu’en résistance
des matériaux); ce nouveau tenseur prend le nom de tenseur des contraintes effectives qui gouvernent
à lui seul le comportement du squelette granulaire et du sol.
Donc, on a :
s’ = s - u
avec :
s = contrainte totale et u = pression
interstitielle
Le
postulat de Terzaghi est un résultat expérimental et non théorique, valable
pour le cas de 2 phases (sol-eau ou sol-air), dans le cas général le problème
est complexe (existence de 3 phases), certes, on peut définir des contraintes
effectives s’, plusieurs tentatives à
citer parmi elles, celle de Bishop :
s’ = s - u0 + x. (ua - uw)
avec : ua = pression de
l’air ; uw = pression de l’eau ; sol saturé x =1 et sol sec x = 0
I.2.Cas statique
|
I.3.Cas d’un écoulement
En statique, une particule de sol n’est soumise qu’à deux forces, son poids et la poussée d’Archimède, par contre en écoulement, la particule sol sera soumise à une force supplémentaire qu’on appelle force d’écoulement.
a) Ecoulement descendant
|
||
|
 |
| Figure 2 : écoulement descendant |
On
déduit qu’un écoulement descendant fait augmenter la contrainte effective (s’). Un remblai inondé lors d’une crue, tasse
à la décrue.
b) Ecoulement ascendant :
Pour un écoulement de sens opposé (ascendant), on
peut montrer que : s’= (g’ - i gw) . z
Lorsque la charge (h) augmente, le débit (Q)
augmente et par conséquent la contrainte effective (s‘) diminue. Cette dernière s’annule quand le
gradient hydraulique i atteint la valeur de
iC = g’ / gw
|
|
 |
| Figure 3 : écoulement ascendant |
Ø à cet
effet, les grains de sol sont parfaitement indépendants et entraînés : c’est le
phénomène de la boulance (ou Renard)
Ø le sol
à cet instant n’offre aucune résistance : Le sol s’est liquéfié
Ø on peut
s’opposer à ce phénomène, soit par :
·
le rabattement de la nappe (diminution de la
charge h ¯)
·
le chargement du fond de fouille augmentation
de s‘ et on aura :
s’=
( g’-
i gw
).z + S avec : S = surcharge à ajouter
II. CONTRAINTES GEOSTATIQUES
Les contraintes dans le
sol sont causées par les charges extérieures appliquées au sol et le poids de
sol. La distribution des contraintes causées par les charges appliquées est
souvent compliquée. La distribution des contraintes causées par le poids propre
au sol peut aussi être compliquée.
Cependant, il existe une
situation commune dans laquelle le poids du sol donne une distribution de
contraintes très simple, cette situation se présente quand la surface du
sol est horizontale et quand, la nature du sol varie peu dans la direction
horizontale. Elle existe fréquemment spécialement dans les sols sédimentaires.
Dans cette situation les contraintes sont appelées contraintes géostatiques.
II.1.Contraintes géostatiques verticales
Dans la situation décrite,
il n’y a pas de contraintes de cisaillement qui agissent sur les plans horizontaux
et verticaux. La contrainte géostatique verticale à n’importe qu’elle
profondeur est alors simplement calculée en considérant le poids du sol qui
agit à cette profondeur.
Si le poids unitaire du
sol est constant avec la profondeur :
sV = g . z , avec g est le poids unitaire du sol et z la profondeur
considérée.
Dans ce cas, la contrainte
verticale varie linéairement avec la profondeur, comme montré sur la figure. Si
le sol est stratifié, le poids unitaire est différent pour chaque couche :
sV = òg.dz = å gi . z i
II.2. contraintes géostatiques horizontales
Le rapport entre les
contraintes horizontale et verticale est appelé le coefficient de contrainte
latérale et est noté par le symbole K :
K
= sh / sV
La définition de K est
utilisée pour des contraintes quelqu’elles soient (géostatiques ou non) .
Souvent, on peut être
intéressé par la valeur de la contrainte géostatique horizontale, dans le cas
spécial où il n’y a pas eu de déformation horizontale dans le dépôt. Dans ce
cas, nous parlons de coefficient de contrainte latérale au repos ou plus
brièvement de coefficient des terres au repos. On utilise alors le symbole «Ko» : sH = K0 . sv
Quand un sol sédimentaire
se forme, il y a un accroissement de la contrainte verticale au futur et à
mesure de la formation du dépôt. Lors de la formation de ce dépôt, qui se fait
généralement sur de grandes étendues, il n’y a pas de raison pour qu’il y ait
une compression latérale significative qui se développe dans le dépôt. A partir
de là, on peut supposer que la contrainte latérale est inférieure à la
contrainte verticale. Pour un dépôt de sable qui s’est formé de cette manière,
Ko aura une valeur typique comprise entre 0.4 et 0.5 .
Par ailleurs, il est
évident aussi que la contrainte latérale peut être supérieure à la contrainte
verticale. Ceci est courant dans le cas de sols qui ont été fortement
surchargés dans le passé. En effet, dans ce cas, les contraintes horizontales
sont «emprisonnées », et ne disparaissent pas quand le chargement disparaît,
Ko peut alors atteindre une valeur de 3.
II.3.Contraintes induites par les charges
appliquées : (Principe de superposition)
La théorie de l’élasticité
(linéaire) est souvent utilisée pour le calcul des contraintes induites à
l’intérieur des massifs de sols par les charges extérieures qui leur sont
appliquées. Cette théorie est principalement basée sur l’hypothèse que les
déformations sont proportionnelles aux contraintes, et donc sur la
réversibilité des déformations. La théorie de l’élasticité (linéaire) repose
sur un principe très important qui est le principe de superposition (figure 3).
Ce principe stipule que :
Etat de contrainte å1 ® état de déformation e1
Etat de contrainte å2 ® état de déformation e2
donc
et par superposition :
(å1
+ å2) ® (e1
+ e2)
Ce principe fondamental
dans la théorie de l’élasticité, sera constamment utilisé. En particulier, nous
aurons : sv = g.H
+ Ds v
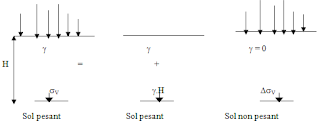 |
| Figure 4 : Principe de superposition |
Où g.H est la contrainte géostatique et Ds v
la contrainte due aux charges appliquées dans un milieu élastique non pesant.
Dans ce chapitre, nous
présenterons aussi deux théories sur le calcul des contraintes dûes à
l’application de charges verticales sur un massif de sol. Ces théories sont
celles de Boussinesq et de Westergaard.
Remarque :
§
La théorie de
l’élastique est une approximation valable pour le calcul des contraintes
verticales. Pour le calcul des autres contraintes, notamment les contraintes
normales horizontales, les résultats peuvent être très irréalistes. C’est pour
cela que nous les donnerons seulement à titre d’information mais il est
recommandé de ne pas les utiliser dans les calculs réels.
§
Il est à noter que
dans les formules dérivées de la théorie de Boussinesq, les contraintes ne
dépendent pas des caractéristiques élastiques du milieu (module d’Young et
coefficient de Poisson du sol), ce qui est un élément favorable à leur
utilisation.
II.4. Théorie
de Boussinesq
La
méthode de Boussinesq repose sur les
hypothèses suivantes : un milieu infiniment large, homogène, isotrope,
semi infini et élastique non pesant chargé par une force verticale Q.
a) Charge ponctuelle
L’application directe de la formule de Boussinesq
pour le cas d’une charge ponctuelle Q à un massif de sol satisfaisant aux
hypothèses de calcul donné pour x situé à la profondeur z :
On peut écrire :
tg q = r / z ; R² = z² + r² ; cos5q =
(z/R) 5
On
obtient : Ds z = 3.Q.z3 / 2p.R5
Qui peut être
aussi écrite :
Dsz=(3Q/2p.Z2)/1/[1+(r/z)²]5/2=Q/z².N
Le facteur
d’influence N = 3 / 2p √ [1+(r/z)²]5/2
Dsv = Ds z = 3Q.cos5q / 2p.z²
Les
valeurs de N pour différentes valeurs de r/z sont données par le tableau
suivant :
r/z
|
N
|
r/z
|
N
|
r/z
|
N
|
0.00
0.10
0.20
0.30
0.40
0.50
0.60
0.70
|
0.476
0.466
0.433
0.385
0.329
0.273
0.221
0.176
|
0.80
0.90
1.00
1.00
1.20
1.30
1.40
1.50
|
0.139
0.108
0.084
0.066
0.051
0.040
0.032
0.025
|
1.60
1.70
1.80
1.90
2.00
2.20
2.40
2.50
|
0.020
0.016
0.013
0.011
0.009
0.006
0.004
0.003
|
Tableau 1 : valeurs de N
b) Charges uniformément réparties
On utilise les procédés du calcul intégral. Chaque
élément d’aire porte une charge équivalente à une force concentrée q0.dA (q0
est la densité de chargement) et engendre au point M une contrainte verticale
:
ds = 3. q0.dA.cos5q / 2pZ² ; avec
cosq = Z / R =
Z / √(r² + Z²)
La contrainte totale sera égale à :
s =
(3 /2pZ²)
ò q0.cos5q dA
l’intégrale se fera sur l’aire totale
l’intégrale se fera sur l’aire totale
ü Charge rectangulaire
La contrainte DsV sous le coin d’une
répartition de charges uniformes et rectangulaires est donnée par : DsV = qo. I avec : I = coefficient d’influence
Donc,
connaissant les dimensions L et B du rectangle, et la profondeur Z du point
sous l’un des coins du rectangle, il suffit de calculer m = L/Z et n = B/Z et
déduire du tableau le coefficient d’influence I . On remarquera
ici que m et n sont interchangeables,
la contrainte est donnée par la relation :
Ds V = IV. qo
Pour
tout point situé ailleurs qu’au droit d’un des coins du rectangle la
détermination de Dsz se fait selon le principe
de superposition.
Les
deux exemples ci dessous, illustrent la démarche à suivre :
2
cas se présentent suivant la position du point de recherche de contrainte; à
l’intérieur ou à l’extérieur du rectangle, la contrainte recherchée en est la
somme.
! A la surface, le coefficient
I ne dépend pas des dimensions du rectangle et vaut 0,25
ü Charge circulaire
Dans l’axe d’une charge circulaire uniforme de rayon
r, la contrainte verticale à la profondeur Z est égale à :
Dsz
= q0.[1 - 1 /
(1+(r/z)3/2)] avec J = f(r/z),
Dsz =
q0 . J
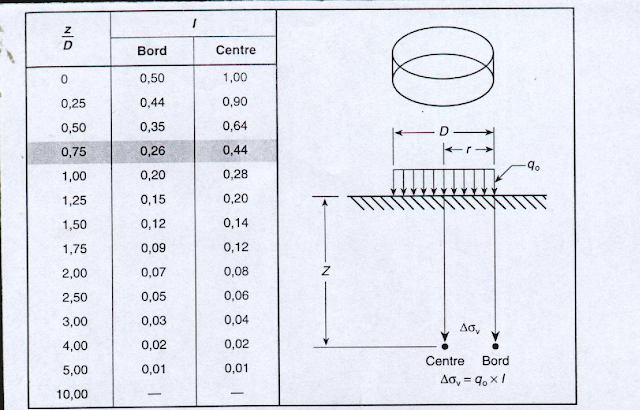 |
| Figure 7 : Charge circulaire |
ü Charge en remblai
La
contrainte à une profondeur z dûe à un remblai sous le coin comme représenté
sur la figure et donnée sous forme d’abaque,
Dsz = I . q0
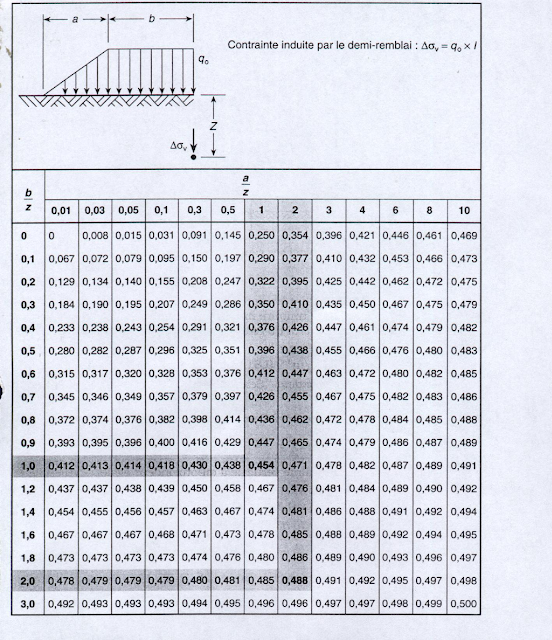 |
| Figure 8 : Charge en remblai |
II.5.Méthode de Newmark
Newmark a construit un abaque, basé sur la solution
de Boussinesq, pour la détermination de la contrainte verticale à n’importe
quel point sous un chargement uniforme q0 de forme quelconque
(complexe ou irrégulier ). A partir de la formule de Boussinesq ; on a :
r/z
= [(1 - DsZ/q0)-2/3 - 1]1/2
On voit bien que chaque abaque est dessiné pour une
valeur de Z donnée, r/z = f(DsZ/q0). Chaque
abaque doit être accompagné d’une échelle AB.
Pour le calcul de la contrainte verticale sous un
point quelconque d’un chargement uniforme quelconque, on doit suivre les étapes
suivantes :
- Dessiner le chargement de densité q0, à l’échelle de l’abaque e = z/Z, avec z la profondeur réelle de calcul et Z la profondeur à l’échelle de l’abaque, c’est à dire Z=AB
- Mettre au centre de l’abaque le point où l’on désire la contrainte verticale.
- Compter le nombre de portions de secteurs comprises dans le dessin soit M.
- La contrainte verticale sous le point en question est alors :
Dsv = M . I . q0
 |
| Figure 9 : Méthode de Newmark |
II.6.Diffusion simplifiée des contraintes
Lorsqu’on ne cherche qu’une valeur approximative des
contraintes verticales, on peut se contenter de la diffusion simplifiée des
contraintes suivantes :
DszA = q0 / [1 + 2(z/a).tg a] ; avec a généralement prise égale à
30° Dszp=
0
 |
| Figure 11 : Abaque (charge ponctuelle) |
.png)
.png) |
| Figure 13 : Abaque (charge trapézoïdale) |




